コンピュータシステムの理論と実装 (1)

年末年始を利用して、2 年くらい前に買ったこの本を読んでいく。

コンピュータシステムの理論と実装 ―モダンなコンピュータの作り方 | Noam Nisan, Shimon Schocken, 斎藤 康毅 |本 | 通販 | Amazon

NAND ゲートのみが与えられた状態で、論理回路、加算器、ALU、CPU などを自作しつつ最終的にはテトリスが動く OS が出来上がるという触れ込みの本書。本文には実装の指針が示してあるのみでありコーディングは自力で頑張らなくてはいけないので普通に勉強になる一冊。

まとまった時間ができた際に進めては中断し、その間に前やったことをすべて忘れるという一連の流れを 3, 4 回繰り返しており非常によろしくないのでいい加減終わらせたいところ。今回はまず第 1 章の復習をしつつまとめを作っていく。

1 章 ブール論理

NAND ゲート $\overline{x \cdot y}$ をもとに各種のプリミティブなゲートを作成していく。

基本論理ゲート

• まずは Not から。これは Nand($x, x$) = $\overline{x}$ であることからすぐに書ける。

CHIP Not {
    IN in;
    OUT out;
    PARTS:
        Nand(a=in, b=in, out=out);
}

• And もただ NAND を否定するだけでよい (NAND は AND の否定なので)。

CHIP And {
    IN a, b;
    OUT out;
    PARTS:
        Nand(a=a, b=b, out=out1);
        Not(in=out1, out=out);
}

• お次は Or の実装。一見ややこしいが、$\overline{A \cup B} = \overline{A} \cap \overline{B}$ (ド・モルガンの法則だっけ) を考えると Not(And(Not($x$), Not($y$))) であることが分かる。下記コードでは最後に And と Not を用いているが、せっかく Nand ゲートが用意されているのでこちらを使ってもよい。

CHIP Or {
    IN a, b;
    OUT out;
    PARTS:
        Not(in=a, out=nota);
        Not(in=b, out=notb);
        And(a=nota, b=notb, out=out1);
        Not(in=out1, out=out);
}

• Xor (2 入力が異なる場合は 1 を、それ以外は 0 を返す) の実装。And と Or は実装済みなので正準表現を使ってしまうのが分かりやすい。真理値表により、Xor($x, y$) $= \overline{x}y + x\overline{y}$ であることが分かるのでコードは下記のようになる。

CHIP Xor {
    IN a, b;
    OUT out;
    PARTS:
        Not(in=a, out=nota);
        Not(in=b, out=notb);
        And(a=a, b=notb, out=out1);
        And(a=nota, b=b, out=out2);
        Or(a=out1, b=out2, out=out);
}

• マルチプレキサ (セレクタが 0 のときは a を、1 のときは b を出力) の実装。if 文みたいなものだが、このあたりから話がややこしくなってくる。

CHIP Mux {
    IN a, b, sel;
    OUT out;
    PARTS:
        Not(in=sel, out=notsel);
        // 例えば、sel = 0 のとき (a が選ばれるとき)
        Or(a=a, b=sel, out=aout); // aout = a となる
        Or(a=b, b=notsel, out=bout); // notsel = 1 なので bout = 1 となり下の And 式の結果に影響しない
        And(a=aout, b=bout, out=out); // 結果的に aout = a の値が出てくる
}

• デマルチプレキサ (セレクタが 0 なら a の方に入力値を流す、1 なら b の方に入力値を流す) の実装。要はマルチプレキサの逆である。

CHIP DMux {
    IN in, sel;
    OUT a, b;
    PARTS:
        Not(in=sel, out=notsel);
        And(a=in, b=notsel, out=a); // a は in と not(sel) との And
        And(a=in, b=sel, out=b); // b は in と sel との And
}

多ビットの基本ゲート

本書で作るのは 16bit の OS なので、上で作った基本ゲートを 16bit に拡張していく。例えば Not16.hdl は以下のようになる。1bit 版のものを 16 個羅列すればいいだけなので特に難しいところはない (タイピングは面倒だが)。多ビットマルチ/デマルチプレキサも選択は 1bit で行うので注意。

CHIP Not16 {
    IN in[16];
    OUT out[16];
    PARTS:
        Not(in=in[0], out=out[0]);
        Not(in=in[1], out=out[1]);
        Not(in=in[2], out=out[2]);
        Not(in=in[3], out=out[3]);
        Not(in=in[4], out=out[4]);
        Not(in=in[5], out=out[5]);
        Not(in=in[6], out=out[6]);
        Not(in=in[7], out=out[7]);
        Not(in=in[8], out=out[8]);
        Not(in=in[9], out=out[9]);
        Not(in=in[10], out=out[10]);
        Not(in=in[11], out=out[11]);
        Not(in=in[12], out=out[12]);
        Not(in=in[13], out=out[13]);
        Not(in=in[14], out=out[14]);
        Not(in=in[15], out=out[15]);
}

多入力の基本ゲート

• 2 入力の基本ゲートを一般化する。例えば $n$ 入力 Or ゲートの場合、入力 $n$ ビットのうち少なくとも少なくとも一つが 1 であれば 1 を出力する形になる。

CHIP Or8Way {
    IN in[8];
    OUT out;
    PARTS:
        Or(a=in[0], b=in[1], out=out1);
        Or(a=out1, b=in[2], out=out2);
        Or(a=out2, b=in[3], out=out3);
        Or(a=out3, b=in[4], out=out4);
        Or(a=out4, b=in[5], out=out5);
        Or(a=out5, b=in[6], out=out6);
        Or(a=out6, b=in[7], out=out);
}

• 次に $m$ 入力のマルチプレキサを考えると、$m$ 個の入力中から 1 個を選択して出力する形になるので選択ビットは $k = \log{m}$ となる。例えば $m = 4$ の場合 $k = 2$ である。実装はマルチプレキサを 2 つ組み合わせればよく、sel[0] を用いて a vs b と c vs d でトーナメント 1 回戦を行ったのち、sel[1] で 2 回戦をやるイメージでいける。

CHIP Mux4Way {
    IN a, b, c, d, sel[2];
    OUT out;
    PARTS:
        Mux(a=a, b=b, sel=sel[0], out=aorb);
        Mux(a=c, b=d, sel=sel[0], out=cord);
        Mux(a=aorb, b=cord, sel=sel[1], out=out);
}

• 最後に $m$ 出力のデマルチプレキサを考える。入力を $m$ 個の出力先に振り分けることになるので、選択ビットは上記同様 $k = \log{m}$ である。

CHIP DMux4Way {
    IN in, sel[2];
    OUT a, b, c, d;
    PARTS:
        // まず、a, b と c, d のどちらかであるかを決めてしまう
        DMux(in=in, sel=sel[1], a=w1, b=w2); // sel[1] = 0 なら w1 = in、sel[1] = 1 なら w1 = 0
        // 以下で、sel[1] = 0 なら w1 = in が正しく a か b かどちらかに振り分けられるし、
        // sel[1] = 1 なら、そもそも w1 = 0 なので a も b も 0 になるという仕組み
        DMux(in=w1, sel=sel[0], a=a, b=b); 
        DMux(in=w2, sel=sel[0], a=c, b=d);
}

検証

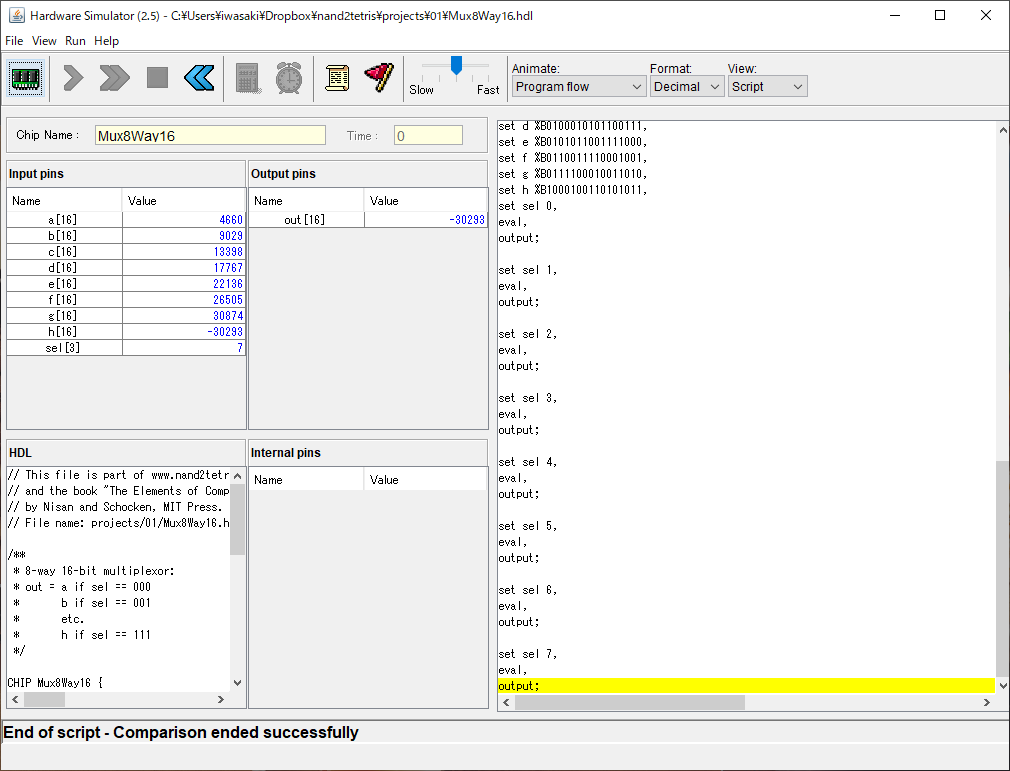
本書の良いところは、公式サイト にあるツールを用いれば書いたコードの検証ができるところである。今回のコードは Hardware Simulator というソフトウェアの Load Script から .tst ファイルを取り込めば一通りのテストが実行できる。

テストをすべて pass するとこんな感じでステータスバーにその旨が表示されるので、競プロで AC した感じがして楽しい。やったね！